关于负电阻的原理及应用的探究
一、负电阻是什么
一般来说,电压随电流变化的情形在纯电阻电路中可使用微分电阻R进行表示:
$$
R={dV\over dI
}
$$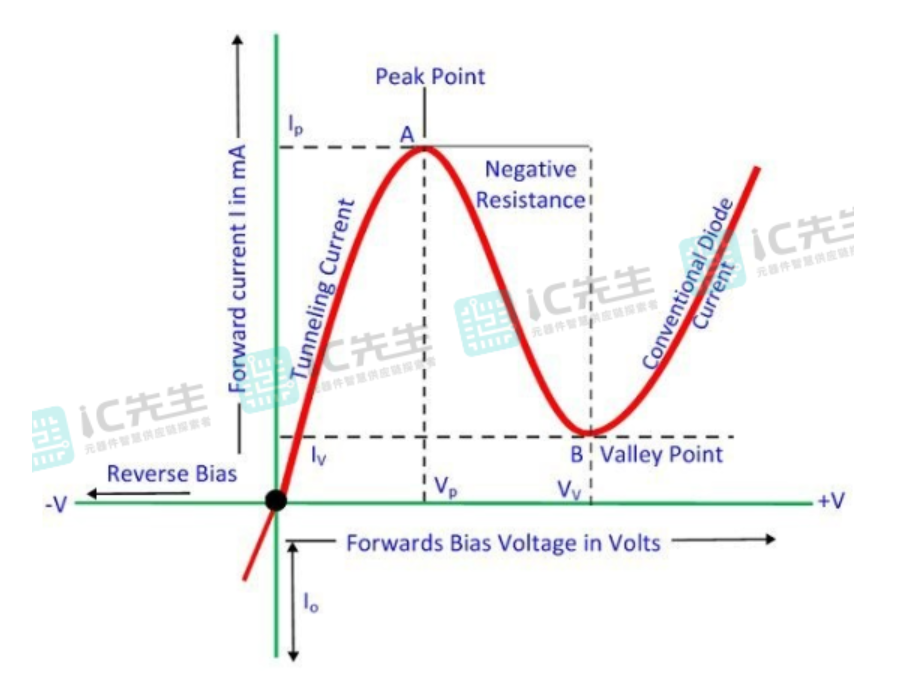
由该图可看出,隧道二极管在A-B的阶段是符合前文所说的负微分效应的,但由于隧道二极管的该区域伏安特性并非线性所以该区域并不能称之为负电阻。
接下来,我们再对负电阻做更加细致的定义:
根据欧姆定律可知电阻二端的电压和电流成正比,其电流-电压关系的图形斜率为正,且会通过原点。
那么就可推导理想负电阻其电流-电压关系的图形斜率为负,且会通过原点,因此只在图中的第二和第四象限出现。
故可对该理想负电阻进行绘制伏安特性曲线:
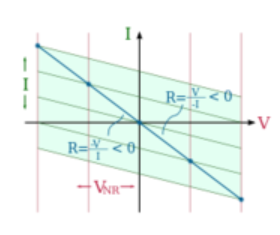
由以上推论及实际现象定义负电阻,即可简单定义为理想的负电阻应该为伏安特性曲线为线性且为斜率为负并经过原点的一种元件。
历史以往研究时有注意到气体放电元件及一些真空管(例如负耗阻性管)会有负阻效应。不过实用且有经济效益的元件一直到固态电子技术普及后才出现。典型的负阻抗电路—负阻抗变换器—是由约翰·林维尔在1953年发明。而典型差动电阻为负值的元件—隧道二极管—则是由江崎玲于奈在1958年发明。
二、实际负电阻元件构建
集成电路兴起后,运算放大器由于其”虚短“”虚断“的特性,为构建一些理论中的器提供了巨大帮助,负电阻也在此应运而生。
负电阻实际元件
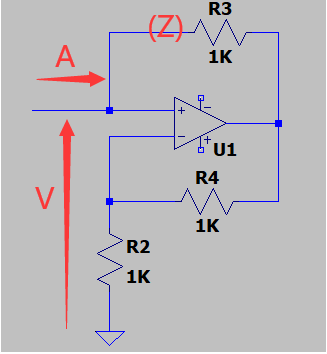
该图像为较为典型的负阻抗电路,其阻抗为:
$$
Z_i = {V\over A} =-Z
$$
现在规定图中电流电压方向为正,由于运算放大器“虚断“的性质,我们可知该电路输入阻抗的绝对值为:
$$
|Z|=R_3
$$
那再由运放的”虚短“性质可知,可以看出该电路形成了一个放大倍数为两倍的同向放大器,所以当输入端设置电压为V时,输出端电压为2V所以此时R3上的电流在我们设定的状态下应该为-A。所以此时有:
$$
-A={V\over R}
$$
该公式可直接推出该电路阻抗为
$$
Z_i = {V\over A} =-Z
$$
从本质上来看,我们会发现这里是通过改变电流方向实现的一种模拟负电阻的电路。那我们该如何验证其是否是负电阻呢?接下来进行仿真。
三、仿真验证
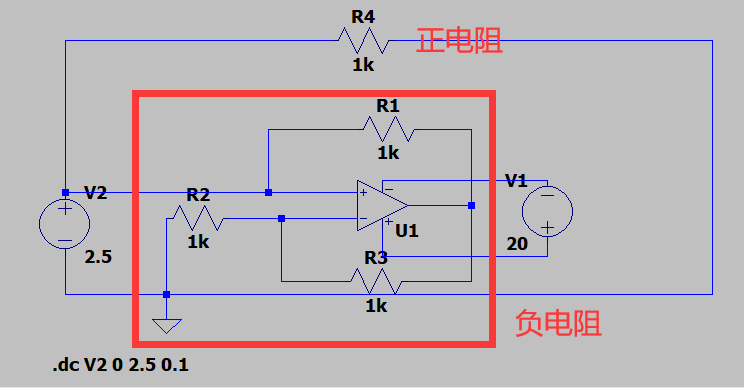
使用 LTspice的直流扫描分析,设置V2从0V开始到2.5V步进0.1V,并给负电阻并联一个正电阻,那么由叠加定理可知,在理想电流源的情况下,正电阻与负电阻上所经过的电流应当相反。那么,开始仿真,测量两个电阻上所经过的电流。
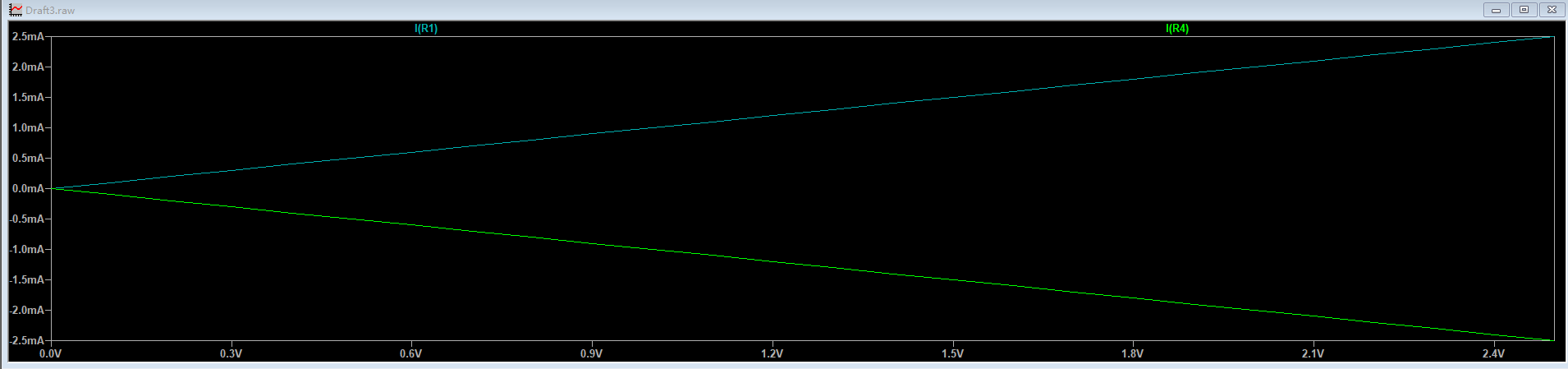
由测试直流分析可以看出,正电阻与负电阻的电流相反,且电流绝对值都为线性上升,所以,在该理想状态下,负电阻能够完美符合我们在前文中的标准。
四、负电阻应用场景
4.1 负阻抗缓冲器
实际使用运算放大器时,我们往往会遇到运放驱动能力不足的情况,这种情况下,我们总是达不到我们所期望的电路效果。通常,当我们遇到这种情况时,我们通常使用一级跟随器(单位增益缓冲)。在这里我们可以尝试使用另外一种方式,即负阻抗缓冲器。当负载阻抗较小时,我们可以通过计算在输出端并联一负阻抗,此时输出阻抗趋于∞,且电路输出信号不会出现衰减的情况。
与传统跟随器方案相比,该方案具有一重要优点,其使负载阻抗变得很大,几乎消除了负载电阻对电路的影响。
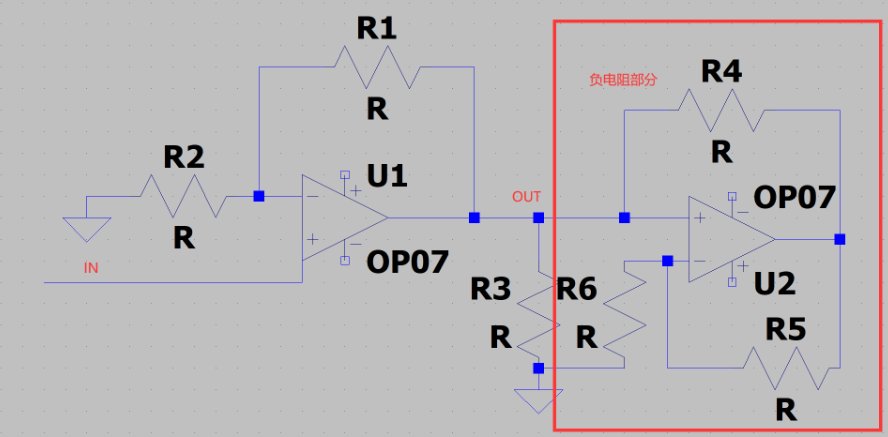
4.2 高输入阻抗放大电路
在进行运放电路的使用时,我们知道同相放大器具有输入阻抗高的特点,而反相放大器具有运放输入端虚地,电路工作稳定的特定。所以,我们是否能通过负阻抗缓冲器的原理类比出高阻抗的反向放大电路呢?答案是可以实现的,通过反向在输入端并联负阻抗电路,即可有效提高输入阻抗。设计方案如下:
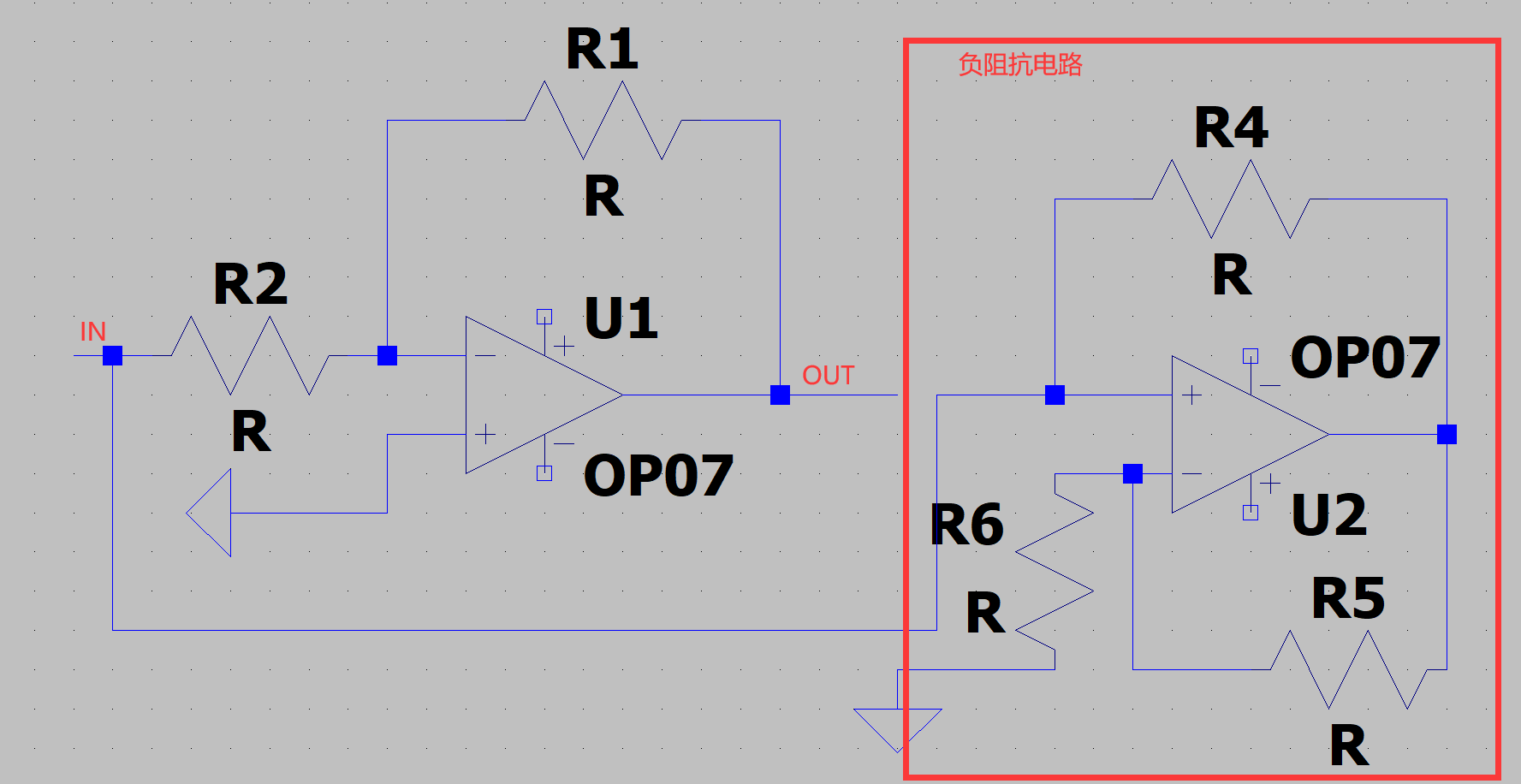
4.3 负电阻在LC振荡电路中的应用
RLC二阶电路的响应具有振荡的特性,特别地,当R = 0 时,电路的响应为无阻尼振荡。为了得到无阻尼振荡特性,可用负电阻来“中和”电路中的正电阻。
通过修改R4,可观察输出端波形幅值的衰减、稳定、增长的现象。 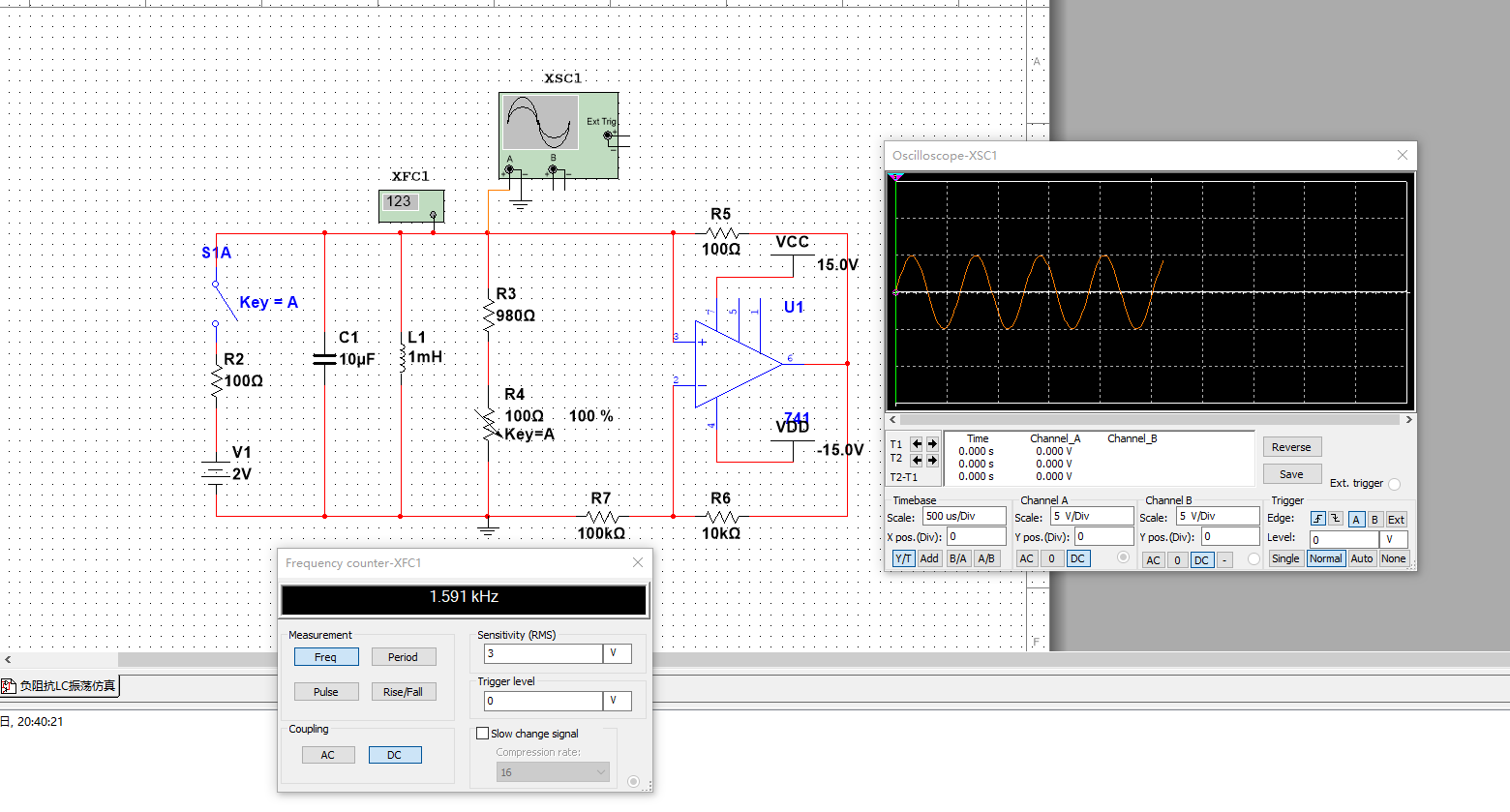
仿真文件地址:img/负阻抗LC振荡仿真.ms14 at master · LILONGXIN178/img (github.com)

