ADC、DAC的理论信噪比计算

一、量化噪声模型以及转换器理论信噪比公式推导

​ 理想转换器对信号进行数字化时，最大误差为±½ LSB，如图的一个理想N位ADC的传递函数所示。对于任何横跨数个LSB的交流信号，其量化误差可以通过一个峰峰值幅度为q (一个LSB的权重)的非相关锯齿波形来近似计算。对该近似法还可以从另一个角度来看 待，即实际量化误差发生在±1/2* q范围内任意一点的概率相等。虽然这种分析不是百分之百 精确，但对大多数应用是足够准确的。

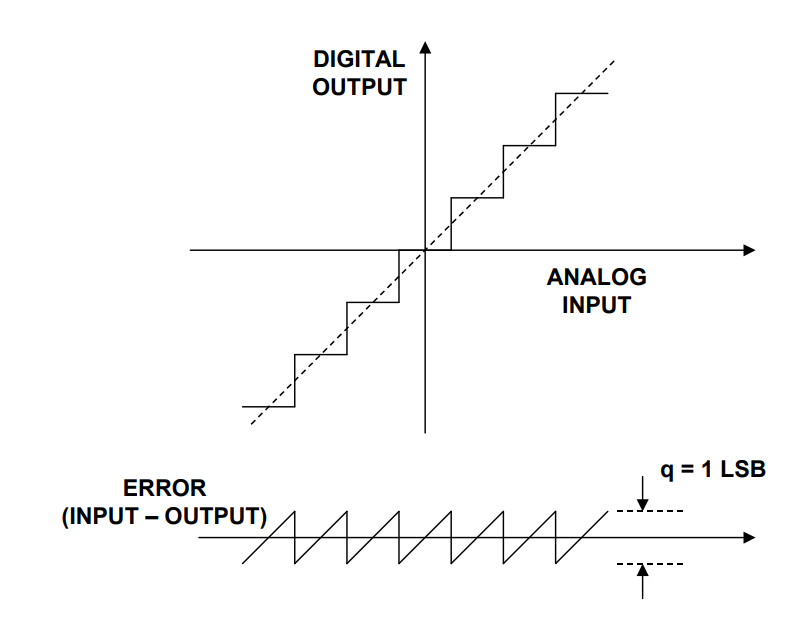
​ 有一种更详细地显示了量化误差与时间关系的图像。

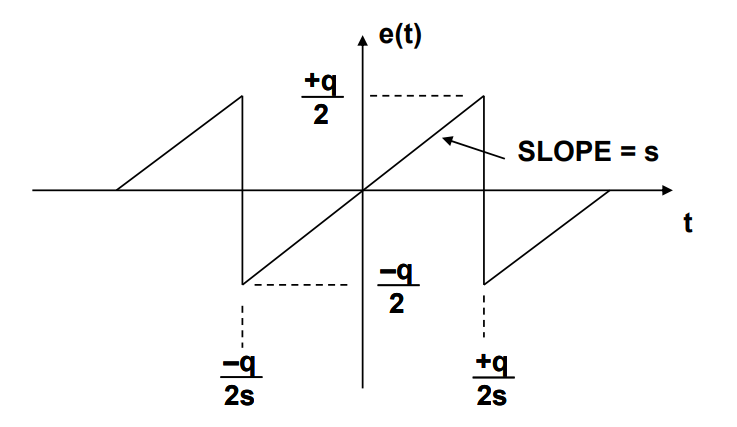
​ 同样，一个简单的锯齿波形就能提供足够准 确的分析模型。锯齿误差的计算公式如下：
$$
\mathrm{e(t)=st,-q/2s<t<+q/2s}
$$
​ e(t)的均方值可以表示为：
$$
\overline{\mathrm{e}^2(t)}=\frac{\mathrm{s}}{\mathrm{q}}{\int_{-\mathrm{q}/2\mathrm{s}}^{+\mathrm{q}/2\mathrm{s}}(\mathrm{s}t)}^2\mathrm{dt}
$$
​ 进行简单的积分和简化可得：
$$
\overline{\mathrm{e}^2(t)}=\frac{\mathrm{q}^2}{12}.
$$
​ 因此，均方根量化误差为：
$$
均方根量化噪声=\sqrt{\mathrm{e}^2(t)}=\frac{\mathrm{q}}{\sqrt{12}}
$$
​ 锯齿误差波形产生的谐波远远超过DC至f s /2的奈奎斯特带宽，然而，所有这些高阶谐波必 须折回(混叠)到奈奎斯特带宽并相加，产生q/√12的均方根噪声。

​ 量化噪声近似于高斯分布，几乎均匀地分布于从DC至 f s /2的奈奎斯特带宽。这里假设量化噪声与输入信号不相关。在某些条件下，当采样时钟和信号通过谐波相关时，量化噪声将与输入信号相关，能量集中在信号的谐波中，但均方 根值仍然约为q/√12。理论信噪比现在可以通过一个满量程输入正弦波来计算：
$$
满量程输入正弦波=\mathrm{v(t)=\frac{q2^N}2\sin(2\pi ft)}
$$
​ 因此，输入信号的均方根值为：
$$
满量程输入的均方根值=\frac{\mathrm{q}2^{\mathrm{N}}}{2\sqrt{2}}
$$
​ 因此，理想N位转换器的均方根信噪比为：
$$
\mathrm{SNR}=20\log_{10}\frac{\text{rms value of FS input}}{\text{rms value of quantization noise}}
$$

$$
\mathrm{SNR=20\log_{10}\left[\frac{q2^N/2\sqrt{2}}{q/\sqrt{12}}\right]=20\log_{10}2^N+20\log_{10}\sqrt{\frac32}}
$$

$$
\mathrm{SNR}=6.02\mathrm{N}+1.76\mathrm{dB}
$$

​ 虽然量化噪声的实际频谱相当复杂，难以分析，但推导出的简化分析对大多数应用足够准确。然而，必须再次强调，均方根量化噪声是在DC至fs/2的完整 奈奎斯特带宽范围内进行测量。

二、峰峰值分辨率与有效分辨率

​ 低带宽、高分辨率ADC的分辨率为16位或24位。但是，器件的有效位数受噪声限制，而噪声则取决于输出字速率和所用的增益设置。有些公司规定使用有效分辨率来表示该参数。

​ 下图显示模拟输入接地时从一个Σ-Δ型ADC获得的典型直方图。理想情况下，对于这一固定的直流模拟输入，输出码应为0。但是，由于噪声影响，恒定模拟输入存在一个码字分布。此噪声包括ADC内部的热噪声和模数转换过程引起的量化噪声。

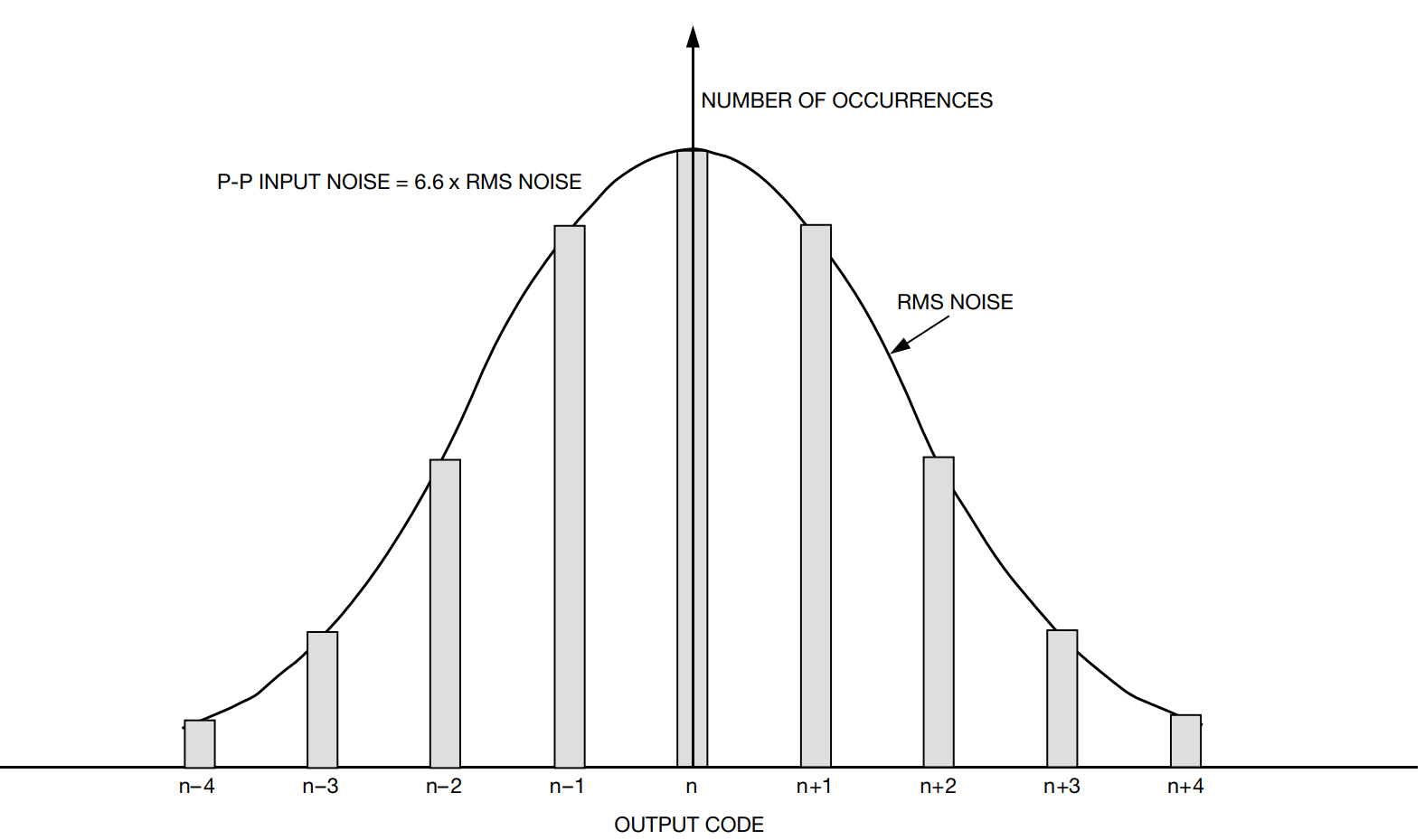
​ 码字分布一般为高斯分布。均方根噪声是通过从该直方图产生的曲线计算出的，曲线的宽度决定均方根噪声。高斯曲线的分布是从负无穷大到正无穷大。然而，99.99%的码 字出现在6.6倍均方根噪声范围内。因此，峰峰值噪声为均方根噪声的6.6倍。

​ 数据手册一般使用均方根噪声。噪声取决于所用的滤波器 频率和增益设置。通常，当模拟输入范围缩小时，均方根噪声也会变小。但是，由于满量程模拟输入信号也被减 小，因此有效位数降低。

​ 假设当模拟输入范围为+2.56 V且，均方根噪声等于1.25μV。根据该数据计算信噪比：
$$
(20\mathrm{log}((6.6\times1.25\text{E-6})/(2.56\times2))=-115.85\mathrm dB
$$
​ 据此计算峰峰值分辨率：
$$
115.85=6.02\mathrm{N}+1.76=>\mathrm{N}=(115.85-1.76)/6.02=19\mathrm Bits
$$
​ 因此，在上述条件下，19个MSB中无闪烁位。 有些公司规定使用有效分辨率，而不是峰峰值分辨率。有效分辨率是通过均方根噪声而非峰值噪声计算出的。使用均方根噪声计算信噪比：
$$
(20\mathrm{log}((1.25\text{Е-}6)/(2.56\times2))=-132.25\mathrm dB
$$
​ 据此计算有效分辨率：
$$
\begin{aligned}132.25&=6.02\mathrm{N}+1.76=>\\\mathrm{N}&=(132.25-1.76)/6.02=21.7\mathrm Bits \end{aligned}
$$
​ 因此，有效分辨率 = 峰峰值分辨率 + 2.7位。 评估ADC时，应当认识到有效分辨率与峰峰值分辨率的计算方法 不同，有效分辨率比峰峰值分辨率大2.7位。此外，有效分辨率没 有突出闪烁位数，峰峰值分辨率则指出了不闪烁的位数，因而能 更好地表示性能。

​ 对于一个ADC，其有效分辨率比峰峰值分辨 率高2.7位。因此，对于有效分辨率为22位的器件，其无闪烁分辨率为22 – 2.7 = 19.3位。要了解器件对于一项应用的真正性能，必须确定所规定的是峰峰值分辨率还是有效分辨率。