信号完整性基础（一）

信号完整性理论就是非常典型的建立数学模型来分析和预测电路实际行为的理论。它有两大两大理论基石：麦克斯韦电磁理论和傅里叶变换：

麦克斯韦的电磁理论描述的是电磁场量之间的相互关系，描述了理想阻、容、感元件在电磁场中行为；
傅里叶变换：任何连续周期信号可以由一组适当的正弦曲线组合而成。

时域与频域

时域：一般来说，时间是物质存在的一种客观形式，由过去、现在、将来构成的连绵不断的系统，是物质的运动变化的持续性和连续性的表现。我们从时间的角度来看事物的变化，这就是所谓的时域。

1，傅里叶与频域

傅里叶变换，表示能将满足一定条件的某个函数表示成三角函数或者它们的积分的线性组合；时域中的任何波形都可由正弦波的组合而成。
傅里叶变换将信号成功的从时间维度（时域）转换成了频率维度（频域），提供给我们一个全新的观察角度，能更加容易的去理解和解释发生的现象。

主要是正弦波有如下的四个性质：

时域中的任何波形都可由正弦波的组合，完全且唯一的描述；
任何两个频率不同的正弦波都是正交的，可以将不同的频率分量相互分离开；
正弦波有精确的数学定义；
正弦波及其微分值处处存在，没有上下边界。

这些性质并不是正弦波所独有，使用正弦波来描述时域信号还有其它好处，它完美的契合了现实电路中的特性和现象：

电路一般用R，L，C组合来表征，这些元件的二阶线性微分方程的解是正弦波；
频域中不会产生新的信息，与时域描述所包含的信息完全相同；
在频域中对一些问题的理解和描述更加容易：

1, 带宽：描述与信号、测量或互连相关的最高有效正弦波频率分量；

2, 阻抗：电源地分布阻抗对电源轨道塌陷问题提供更简单的解释和解决方法；
—— 轨道塌陷噪声（Rail Collapse Noise）通常指电源轨上的电压瞬时跌落现象，
3, 电磁干扰：产品的电磁兼容问题使用频域更加容易定位解决；

4, 有损传输线损耗分析：串联电阻随频率的平方根增加，介质内并联交流漏电（介质损耗）随频率线性增加。

2，时域到频域的转换

正弦波是频域中唯一存在的波形，它在时域中需要标记很多的电压-时间数据；而在频域中它只需用3项描述：频率、幅度和相位。
对于有若干频点的实际信号波形，可以通过傅里叶变换转换成频域，这样可以很直观的观察到各个频点频率以及能量大小。

假设有一个1GHz的理想数字信号波形-方波：信号上升沿为0，占空比为50%；频谱中正弦波的频率是1GHz的整数倍，所有偶次谐波分量幅度都为0，只有奇次谐波有幅度：An = 2/(nπ)（如下右图傅里叶变换后可以得到该结论）。其中有一个特殊频点：0Hz，它表示了直流偏移分量，其幅度等于信号平均值。如下图所示，由傅里叶变换计算可得1次谐波的信号幅度为0.63V，加上直流偏移分量：0.5V，那么它的幅度会大于理想方波自身的幅度（违反直觉，但从能量的角度能够解释）。
——如上右图所示，正常信号波形并非只有奇次谐波能量，偶次谐波上同样存在能量分布（所以EMI也要关注信号的偶次谐波分量）；而如下左图的理想方波（且占空比为50%）的情况下，偶次谐波的能量为0。

3，频域逆变到时域

根据傅里叶变换的原理，我们将频域上的所有谐波频率（无限）正弦波叠加起来，就能得到从能量角度来看无限逼近的理想方波；如下图所示，我们每次叠加一部分谐波频率分量，在这个过程的波形中，可以得到如下三个结论：

随着叠加谐波频率越大，信号边沿时间越短（越陡）；
随着叠加谐波频率越大，信号电平幅度越稳定（越接近原始波形电平幅度）；
随着叠加谐波频率越大，越接近理想方波。

信号边沿时间与叠加的最高谐波频率分量相关，以理想方波频谱为基准，波形最高频率分量越大，10%-90%（或20%~80%）边沿就越短。
那么，我们怎么来确定信号最高频率分量？那就必须引出另一重量级概念：带宽。

带宽

带宽并非是数据速率，而是指信号不失真情况下的频谱宽度。
带宽是指：表示频谱中最高的有效正弦波频率分量值，所有高于带宽的频率都可忽略不计。

但实际电路中不会存在一个界限：小于某一频点无损通过，而大于某一频点是100%衰减；往往衰减量对相对频率是连续的，一般定义最高有效正弦波频率分量指的是：在信道传递函数的伯德图中下降3dB的频率点，我们称之为该信道的带宽。

1，有效带宽0.35/tr

首先，我们给出一个理想方波上升沿，即阶跃信号。而实际方波仍有上升沿时间，由傅里叶变换可知，其为有限次谐波的方波信号。那么假设，我将阶跃信号通入RC低通滤波器这一系统中，理论上输出的信号Vo应为有限次谐波的方波信号。
所以只要建立起滤波器、方波频谱以及滤波后信号波形上升时间的关系，就能得到信号上升时间与带宽的关系。

如果Vin 是一个0~1V的阶跃信号，则Vout 就是该滤波网络的阶跃响应。根据电路理论可知
$$
V_{out} = 1-\mathrm{e}^{-\frac{t}{\tau_{RC}}}
$$
其中，τRC =RC为该网络的时间常数。阶跃响应如图所示。

定义Tr 为信号幅度的10%-90%所对应的时间跨度，即10%90%上升时间，则Tr 可以通过如下方式计算得到：
$$
0.9=1-\mathrm{e}^{-\frac{t_{90}}{\tau_{RC}}}\Rightarrow t_{90}=-\ln0.1\bullet\tau_{RC}\0.1=1-\mathrm{e}^{-\frac{t_{10}}{\tau_{RC}}}\Rightarrow t_{10}=-\ln0.9\bullet\tau_{RC}
$$
进而得到10%90%上升时间与电路时间常数τRC 的关系

$$
T_r=t_{90}-t_{10}=\tau_{RC}\cdot\ln\frac{0.9}{0.1}=2.197 2\tau_{RC}
$$
接下来看滤波器的频域特性，RC网络的频域响应可表示为
$$
H(f)=\frac1{1+\mathrm{j}2\pi fRC}=\frac1{1+\mathrm{j}2\pi f\tau_{{RC}}}
$$
幅度为
$$
\left|H(f)\right|=\frac{1}{\sqrt{1+\left(2\pi f\tau{{RC}}\right)^{2}}}
$$
其频率响应如图所示。在响应幅度的-3dB处，|H（f）|下降为最大值的$\frac{1}{\sqrt{2}}$ ，此时有
$$
\begin{aligned}2\pi f\tau{{RC}} & =1\f{{3dB}} & =\frac{1}{2\pi\tau{_{RC}}}\end{aligned}
$$

代入该式到上文中的公式，可推导出：
$$
f_{\mathrm{3dB}}=\frac{1}{2\pi} \frac{1}{\tau_{\mathrm{RC}}}=\frac{1}{2\pi} \frac{2. 197 2}{T_{r}}=\frac{0. 35}{T_{r}}
$$
由此可得，0.35/tr实质上是单极型低通滤波网络的3dB带宽。需要特别说明的是，这种带宽定义方式中，Tr 指的是10%~90%信号上升时间。

2，有效带宽0.5/tr

定义一个系统带宽，可以使用3dB带宽，也可以使用等效噪声带宽或称为均方差带宽，记为$f_{RMS}$ 。对于单极型低通滤波网络， 0.5/tr与等效噪声带宽很接近。如果给定系统的频域传输函数为H（ω），则等效噪声带宽$f_{RMS}$可表示为
$$
f_{\mathrm{RMS}}=\frac{1}{2\pi}\int_{0}^{\infty}\left|\frac{H(\omega)}{H_{\mathrm{max}}}\right|^{2}\mathrm{d}\omega
$$
其中，Hmax 为H（ω）的最大值。为了弄清楚fRMS 的含义，将定义变形
$$
2\pi f_{\mathrm{RMS}} \left| H_{\mathrm{max}} \right|^{2}=\int_{0}^{\infty} \left| H(\omega) \right|^{2}\mathrm{d}\omega
$$
等效噪声带宽fRMS 是这样一种频带宽度：如果频谱在该带宽定义的频率范围内幅值不变，保持频域传输函数为H（ω）的最大值Hmax ，则该频带内$|H_{\max}|^{2}$下所覆盖的矩形面积等于$|H_{\max}|^{2}$ 在整个频率范围内覆盖的面积，

对于单极型低通滤波网络，3dB带宽f3dB 与等效噪声带宽$f_{RMS}$ 之间有着确定的关系。下面我们通过简单的数学推导找出这种关系。将单极型RC滤波网络的传输函数写成如下形式：
$$
H(\omega)=\frac1{1+\mathrm{j}\frac\omega{\omega_{3\mathrm{dB}}}}
$$

$$
\left|H(\omega)\right|=\frac{1}{\sqrt{1+\left(\frac{\omega}{\omega_{3\mathrm{dB}}}\right)^{2}}}=\frac{\omega_{3\mathrm{dB}}}{\sqrt{\omega^{2}+\omega_{3\mathrm{dB}}^{2}}}
$$

有Hmax =1，将该式带入上文$f_{RMS}$计算公式中，得：
$$
\begin{aligned}
f_{RMS}& =\frac{1}{2\pi}\int_{0}^{\infty}\frac{\omega_{3\mathrm{dB}}^{2}}{\omega^{2}+\omega_{3\mathrm{dB}}^{2}}\mathrm{d}\omega=\frac{1}{2\pi}\omega_{3\mathrm{dB}}^{2} \frac{1}{\omega_{3\mathrm{dB}}} \arctan\left(\frac{\omega}{\omega_{3\mathrm{dB}}}\right) \bigg|{0}^{\infty} \
&=\frac{\omega{3\mathrm{dB}}}{2\pi} \frac\pi2 \
&=\frac{\pi}{2}f_{\mathrm{3dB}}
\end{aligned}
$$
此时，可得等效噪声带宽与上升时间得关系式：
$$
f_{\mathrm{RMS}}=\frac{\pi}{2}f_{\mathrm{3dB}}=\frac{\pi}{2}\frac{0.35}{T_{r}}=\frac{0.55}{T_{r}}
$$
可见，信号带宽的定义 0.5/tr与单极型低通滤波网络的等效噪声带宽$f_{RMS}$非常接近，相当于等效噪声带宽$f_{RMS}$。如果定义带宽所使用的滤波网络的响应和单极型低通滤波网络不同，那么得到的带宽也不同。

3，其他说法的信号带宽

从原则上讲边沿时间和时钟的唯一约束是：边沿时间一定小于周期的50%。但实际设计中，边沿时间一般要求小于时钟周期的10%，为了带宽计算方便（BW = 0.35/RT），估计边沿时间为时钟周期的7%；
——如此计算时钟带宽：BWclock = 0.35/（0.07*Tclock）= 5Fclock，是信号频率的5倍，或则说最高正弦频率是5次谐波。（这可能是方波采集需要10倍频以上得采样时间得原因【奈奎斯特两倍于五次谐波】）

4，互连带宽

互连带宽是指：能被互连传输且未造成有效损耗的最高正弦波分量。对于有损传输线来说，导线损耗和介质损耗对高频分量的衰减要大于低频分量的衰减，这种选择性衰减使得互连中传播信号的带宽降低。互连的“有效”最高频率分量指的是：传输线频率分量幅度减小3dB（幅值70%左右）。
互连带宽是对互连所能传输信号的最短边沿的度量。
假设互连带宽为1GHz，那么它所能传输的最快边沿RT=0.35/1GHz=350ps（本征边沿时间）；如果边沿时间为350ps的信号进入互连，那么输出边沿时间RT²out = RT²in + RT²interconnect，，RTout = $(\sqrt{350^2 + 350^2})$ = 495ps。
如果要使互连对信号边沿时间的影响不超过10%，那么互连的本征上升沿要小于该信号上升沿的50%，也就是说互连的带宽要大于信号带宽的2倍；为传输1GHz带宽的信号，互连带宽至少需要2GHz。

5,测量带宽

测量带宽是指：对于在时域工作的测量仪器，它的测量带宽取决于它能输出到被测元件的信号的最快边沿；例如，测量所得快速阶跃边沿时间为52ps，那么边沿带宽为0.35/52ps=7GHz，这是时域反射计输出端信号的带宽。
为保证信号能被正确测量，最好使测量的带宽可以超过信号的带宽（5倍频）。

传输线理论

1，传输线电感

仔细观察传输线的电流回路：传输线上的电流只要从源端发出，那么它必然将会回到源端，形成一个的闭环。如下图所示传输线的信号路径（信号电流）与返回路径（返回电流）形成了一个个回路，构成类似电感器的环路结构，这个电感就叫做：回路电感。
——并非是信号从源端传播到了终端后，回流才从终端返回到了源端最终形成一个回路；而是信号在不断向前传播的同时，回流在不断地出现；下面章节会详细分析。

（1）传输线电感定义

电感：L = dφ/dI，即在单位变化电流下在导线内部及其周围产生磁通量（磁力线匝数）的变化；再简单一点表述：电感就是导体电流为1A时周围的磁力线匝数；
假设有这么一段导线，只有这一段有电流，前后都没电流，也没有回流（这种情况实际不存在），那么它有电感么？比照电感的定义，当这段导线通过1A电流时，周围产生了磁力线，因为只要有电流流过，就会产生围绕着电流的闭合磁力线，差别只在于磁力线匝数的不同（没有那么多圈圈来叠加）。那么，这段导线的电感，我们就称它为：局部自感。
——圆杆导线局部自感近似公式：L = 5$\times$Len[ln(2$\times$Len/r)-(3/4)]。

局部自感是局部导线自身的电感，如果有导线a和导线b两条导线相邻，而且导线b中发生电流变化，那么它必然会影响到围绕着导线a的磁力线匝数发生变化，此时所产生的电感就是：局部互感。那么局部自感和局部互感就组成了：局部电感；即电感由：自感和互感组成。
——磁力线只要穿越了导线的周边范围，就必然会与导线自身的磁力线叠加或抵消，根据电感公式可知，其磁力线的大小发生变化则电感量必然发生变化。两根圆杆导线局部互感近似公式：L = 5$\times$Len[ln(2$\times$Len/s)-1]。

传输线在信号传播过程中会形成一个完整的电流回路，其总电感是：回路电感，所以对于回路电感来说，必然由：回路自感和回路互感组成。

（2）传输线电感详解

传输线的电流是从源端发出经过信号路径，再从回流路径返回到源端，形成一个电流环路；如下图所示，那么电流环路的电感由这几部分构成：

信号路径自感（La，局部自感）：信号路径本身的电感；
回流路径自感（Lb，局部自感）：回流路径本身的电感；
信号路径和回流路径互感（Lab，局部互感）：如上图所示，信号路径a产生的磁力线会与回流路径b的磁力线相互影响（叠加或抵消），那么它们之间的相互影响就是互感。

由于回流路径上的电流方向与信号路径相反，用右手定则发现电流相反会减小相邻导线的磁力线匝数，所以此时互感的作用是减小整体电感；因此传输线回路电感：Lloop = （La - Lab）+ （Lb - Lab）= La + Lb – 2*Lab。互感Lab随信号路径与回流路径间距的减小而增加，随着信号频率增加，为减小Lloop（回路自感），使返回路径尽量靠近信号路径并减小回路面积（返回路径在信号路径正下方），从而增大两条路径之间的局部电感（Lab）。
回路互感指的是两条不同传输线之间产生的电感：某一回路中流过单位安培电流时，环绕在另一完整电流回路周围的磁力线匝数；电流方向不同回路互感对回路电感大小的影响不同（电流同向：回路电感=回路自感+回路互感；电流反向：回路电感=回路自感-回路互感）。
——磁力线的圈圈要包围住导线（电流），才能影响导线的电感，如上图中，如果磁力线落在a和b之间，那么是不会影响到导线电感的。

如下为传输线所有的电感定义：

局部电感：其它地方没有电流存在时，环绕在该段导线周围的磁力线匝数。
局部自感：仅在一段导线中有单位安培电流而其他地方无电流存在时，环绕在该段导线自身周围的磁力线匝数。
局部互感：仅在某一段导线中有单位安培电流而其他地方无电流存在时，环绕在另一段导线周围的磁力线匝数。
回路电感：流过单位安培电流时，环绕在整个电流回路周围的磁力线总匝数。
回路自感：完整电流回路中流过单位安培电流时，环绕在该回路周围的磁力线总匝数。
回路互感：某一回路中流过单位安培电流时，环绕在另一完整电流回路周围的磁力线匝数。
有效电感：当整个回路中流过单位安培电流时，环绕在一段导线周围的磁力线总匝数，其中包括源于回路每一部分电流的磁力线。

（3）电感的作用和影响

当周围磁力线匝数发生变化时导体两端会产生感应电动势：V = ΔN/Δt = L$\times$ΔI/Δt = L$\times$dI/dt。导线自身电流变化时，它通过自感产生自感电动势，阻止导线自身电流的变化；
——所以从原理来说，相当于一个电感器的作用，会阻止导线中电流的变化。
如果有相邻导线，则会通过互感在相邻导线上产生感应电动势，从而形成感应电压噪声。
当导线中通过直流电流时，导线中的电流分布是均匀的，计算的磁力线匝数重点关注导线外的磁力线，事实上如下左图的横截面所示导线内部也存在磁力线（上节所述的内电感），是导线自感的一部分；导线内部和外部磁力线圈都会影响自感，我们称它们为：内部自感和外部自感。
如下中图所示当电流聚集在导线的中间I1或则分散在边缘I2（I1 = I2），它们的自感一样么？如下右图所示，I1和I2的磁力线只是分别围绕在I1和I2的外面，I1和I2电流大小相等，那么在I2圈外呈现的I1和I2的磁力线匝数（电感）相同；但是在导线内部I1存在着相比于I2更多的磁力线匝数（内部自感部分），这些多出来的磁力线匝数就是I1相对于I2更大的电感量。

趋肤效应

导线外部的磁力线匝数（外部电感）并不会随着频率的变化而变化，但是导线内部磁力线匝数（内部电感）会随着电流的分布而出现变化。随着频率的增加导线的感抗Z= jωL也随之增加，而电流总是循着最小阻抗的路径流动，当导线感抗与电阻比值随着频率越高越大时，电流便越趋于沿着导线的外表面流动（此时导线内部电感小，减小感抗），这就是趋肤效应。
趋肤效应影响的结果是随信号频率的增大而导线电流趋于分布到导体外表面，影响如下：

导线自感减小，从而减小了传输线的回路电感；
导线电流通过的横截面减小（Z=ρ*L/A），导线电阻增加，线路损耗增加。

随着电流频率的增加，电流流向导线的外边缘，大部分电流集中在一个厚度等于趋肤深度导线的趋肤深度δ的环面中： δ = √(1/σ$\times$π$\times$μ$\times$f)。其中，σ：电导率；μ：磁导率；f：正弦波频率；一般典型的导体都是非铁磁性的，所以μ = μ0 = 4π*10⁻⁷。
——铜线的趋肤深度：δ = 66$\times$√(1/f)μm。

趋肤效应会将电流聚集到导线表面，使得通过导线的实际横截面积减小，那么其必然会增加导线的电阻率（单位长度的电阻大小）。如下图所示，对圆导线的电阻损耗进行分析：

临近效应

趋肤效应是导线自感所导致的一种现象，那两条导线之间的互感会导致传输线什么样的现象？答案是：邻近效应。

信号路径上电流与回流路径上电流的方向是相反的，回路电感=自感-互感；
在高频电流中信号路径与回流路径中的电流分布靠的越近，它们所构成的回路面积就越小（互感越大），从而传输线回路电感就越小。

——电流分布总是趋于低阻抗的路径流动，如果是直流电流呢？那么电感就毫无作用（Z = jωL = 0），所以此时电阻占据主要作用，所以电流就会按照最小电阻的路径来流动（电流平均布满整根导线，实现最低电阻）。

涡流

根据电磁感应原理：在两个相互靠近导体中，一个导体上电流有改变，那么另外一个导体的两端会产生感应电压，同时该感应电压会形成电流；再简单点表述：当其中一个导体电流变化时，另一个导体会产生感应电流，这个感应电流就是涡流。
涡流存在于所有的所有的导体结构，但有一种非常特殊的几何结构：电流回路靠近大的导电平面；假设金属平面（可以不是GND或电源）上方有一个线圈，当线圈中有电流变化时，变化的磁力线就会穿过导电平面，并在平面上激起涡流，这些涡流反过来会影响自己产生的磁力线。

如上右图所示，通过麦克斯韦方程组求解：涡流产生的磁力线结构就像是平面下方的另一电流产生，它与平面的距离和真实电流与平面的距离相等，这个虚构的电流称为：镜像电流。镜像电流与实际电流大小相等，方向相反，而且镜像电流的一些磁力线会环绕在实际电流周围，源于涡流的互磁力线圈将减小导线的总电感，实际上就是减小了线圈的局部电感。
在电感下方铺铜皮（GND或其它），是否能减小其正下方导线的影响？首先，铜线以及FR4介质的磁导率约为1，对电感所产生的磁力线无任何作用，磁力线可以轻易穿透铜皮和介质不会产生衰减，对磁力线产生影响的只是与电感距离的大小，离电感越远磁力线密度越小，互感就越小。
刚刚分析了铜皮会产生涡流，必然会增加了互感，从而减小了电感的感量。如果是开关电源的电感，那么随着电感感量的减小，输出电源纹波电流会增加。另外，铜皮涡流势必会导致电源/GND平面的噪声增加，影响EMI辐射。

2，传输线电容

（1）电容的概念

电容是两块导体中间夹着一块绝缘体构成的电子元件，实际上任何两个绝缘导体之间都有一定的电容量；
如果给两个导体上分别加上正电荷和负电荷，那么两个导体之间会存在电压，那么这一对导体的电容量就是单个导体上存储电荷量和导体之间电压的比值：C = dQ/dV；两个导体在给定电压下储存电荷越多，电容值就越大。
电容中间是绝缘介质材料，两个导体之间不存在直流通路，只有当导体两端电压发生变化时，才会有电流流经电容器：I = ΔQ/Δt = C*dV/dt；这个电流是等效电流（并不是真的有电流从电容中间流过）称之为：位移电流；（在导体中自由电荷的运动称之为：传导电流）。当dV/dt保持不变时，电容容量越大，流过电容的电流就越大，表现出来的电容阻抗就越小。
平行板电容是PCB上的常见电容形式，电容量近似表示为：C = ε0 * εr * A/d；该式表明一个重要的几何结构特征：导体间距越大，电容量越小；重叠面积越大，电容量越大。

（2）介质介电常数

极化的概念，任何物质在电场的作用下都会被极化，如下图所示在外部电场E的作用下，介质内部会产生一个强度为E’的反向电场。由于增加在两个导体上电荷所形成的电场E被介质极化电场E’削弱，所以需要在导体上增加更多的电荷Q才能达到原本的电场强度E0（外在表现为导体间电压），从而增加了电容量；其增加电容量的比例就是相对介电常数：εr = E/E0 = E/(E-E’) = C/C0。

当电介质受到静电场作用时，往往要经过一段时间（磁豫时间/偶极子运动时间）极化强度才能达到其最终值；如果电介质受交变电场作用，而交变电场的改变相当迅速时，极化就会追随不及而滞后，从而导致动态介电常数与静态介电常数之间的不同；当信号频率上升到驰豫极化完全跟不上电场的变化（假设100GHz），只会有瞬时极化发生，此时εr 趋向于 1，且无介质损耗发生；

信号频率变化引起介电常数变化的同时，还会导致介质损耗；由于电介质在电场作用下偶极子会发生移动（从而产生极化），这会导致电场能量的损耗：

随着频率的增加，电场周期变短，短到可以与驰豫时间相比，极化时间逐渐跟不上电场的变化，这时介质损耗也逐渐增加；
同时偶极子运动所产生的极化电流（信号路径与回流路径之间的漏电流/电导）也逐渐增加。
——这是除了趋肤效应外的另一高频损耗，且跟电介质本身特性强相关。

集总和分布模型

对于信号传输来说，其实就是电磁波的传播。所以对于电路长度来说：重要的不是走线电路本身的尺寸（长度），而是电尺寸（电路尺寸/波长）。
波长代表了电磁波相位改变360°时传播的距离。虽然麦克斯韦的方程组可以解释所有的电现象，但太复杂了不便于应用啊。那是否有方法能够简化的呢？

有一种近似的方法：采用集总模型和基尔霍夫定律来分析。即当电路最大尺寸为电小尺寸时。那又如何定义电小尺寸呢？
只要电路尺寸（PCB走线长度）远小于信号波长就行了；一般来说当电路的最大尺寸（走线长度）小于信号最高频率波长的1/10时，就认为是电小尺寸。好，那我们来总结一下：当PCB走线（线缆）长度小于信号最高频率对应的波长1/10时，就认为是集总模型，可以用基尔霍夫定律。

一般情况下，如果连接线长度小于信号激励源频率对应波长的1/10，那么我们就假定相移可以忽略不计。在一些特殊情况下，可能要求更高。
——对电路设计来说，电尺寸比PCB走线长度（电路尺寸）更重要，因为当走线长度小于波长的1/10时，信号经过该距离的传播后的相移可忽略不计，所以此时连接线可认为是电小尺寸。

计算电尺寸来判断一个电路是否为电小尺寸（L < λ/10），如果是电小尺寸，就可以运用比电大尺寸（L > λ/10）更简单的集总参数电路模型，采用基尔霍夫电压和电流定律；如果是电大尺寸（分布参数电路模型），那么只能运用麦克斯韦方程组或则用一系列集总参数电路串行来近似。对于分布参数电路模型来说，电磁波的滞后效应不可忽略，沿线传播的电磁波不仅是时间的函数，而且是空间坐标的函数。

传输线

1，传输线定义

传输线就是：由两条有一定长度的导线组成，把电磁能从电路的一端送到电路另一端的装置。

从传输线的物理结构描述：是由两条有一定长度的导线组成；

两条：从某种意义上来说是对的，因为信号的传输就是通过：信号路径和回流路径，这两条“导线”来实现的；但实际信号传输过程中，特别是回流路径往往并不是简单的一条路径，而是根据其固有物理规律（回路阻抗最小）自行选择的n条回流路径；从另外一层意义上来说：传输线说的就是信号路径与回流路径之间的关系，与其它（电源、地）无关；
——之所以是n条，因为信号路径上的信号频率一般不是单一频率（有很多频率分量等等），所以不同频率分量就对应了不同的回流路径，很难确定具体的回流路径。
一定长度：固定长度的导线对于信号A是传输线，可能对信号B来说就只是导线；对于传输线来说，导线长度与信号的边沿时间强相关，它要满足分布系统模（导线长度大于或等于波长），在短线模式或集总系统中的导线不再是传输线（不适用传输线模型的相关理论），而只是导线(可使用基尔霍夫定律解决)

从传输线的功能描述：把电磁能从电路的一端送到电路另一端的装置；

（1）电磁能：传输线传输的是电磁波；那么什么是电磁波呢？

固定的3.3V电平或0V电平是电磁波么？很明显，固定电平并不会产生电磁波，电磁波的传播只发生在信号发生跳变的一瞬间；
——固定电平只有固定的电场和磁场，而非交替出现的电磁场（电磁波）。
传输线只传输由3.3V变成0V或则0V变成3.3V的这些信号边沿，固定的电平不是传输线所传播的；所以高速还是低速信号的判断不在于信号本身频率的高低，而在于传输信号边沿的快慢（最高频率分量）。
——但是信号本身频率更高，往往意味着边沿跳变更快，它们是有关联的。

（2）从电路的一端送给电路另一端：电磁能的传输需要从发送端传到接收端，需要保证的是接收端信号能够被正确的接收，而不是要求发出端的信号完整，这是传输线的意义所在。
——测试信号质量的时候是选择发送端还是接收端呢？明显是接收端，但一不小心测了发送端，发现发送端的信号质量很差，会不会有问题呢？发送端信号质量差是正常的。

2，传输线工作原理

实际设计中，回流路径往往是回流地或电源，但我们需要明确地将：回流路径的概念与回流地/电源区分开，避免导致概念的混淆。

只有当信号路径相对回流路径有电压跳变时（信号前沿），信号路径上的电流通过互感和电容（信号路径相对于回流路径）流向回流路径（位移电流）；
——需再次强调：传输线模型只使用于跳变信号（信号前沿），对于固定电平，传输线模型的电感和电容不起作用（电感短路，电容开路），此时起作用的只是导线的串联电阻。
假设有一个导线从地球延伸到月球，此时传输线延时约为1.2s（约38万公里）：信号电流从地球向月球传输，返回电流从月球向地球传输形成一个电流环路，那么返回电流是信号电流到达月球后，再从月球发送回来的么（总共经过2.4s）？

当信号电流从地球（源端）发出的瞬间，就开始对传输线电容进行充电：电流从芯片电源->芯片驱动管脚->信号路径->电容->回流路径->芯片电源，形成一个完整的回路，即返回电流是跟随信号电流即时产生的；
信号还未传到远处时，它还不知道后面的传输线结构如何，电流已经过返回路径回到源端，仅仅与信号前沿的环境（介电常数和磁导率等）和信号前沿所在的那一小段传输线有关；
一旦信号路径中信号发出，回流一直存在，直到在接收端的回流返回到源端，总共花费时间是：2倍的走线延时（举个栗子：地球与月球之间延时的两倍：2.4s）。

所以可以得到结论

只有在信号前沿（跳变）处的导线才工作在传输线模式，且信号状态只与信号前沿所处位置有关；
——只有信号边沿（特定时间）所占据的那段导线（特定位置）才是传输线；并非导线的任何时刻、任何位置都是传输线。

3，传输线如何回流

传输线的回流路径并非一定要是GND平面，那么对于回流平面不是GND平面的情况下是怎样的呢？
如下图所示，一条带状线（什么是带状线？置于2个平行的地平面（或电源平面）之间的电介质之间的一根传输导线）上层是电源平面，下层是GND平面，那么信号线中传输信号时，它会智能地选择GND平面来作为回流么？

当信号线上的电平由低（0）到高（1）跳变时，其电流通路如下图所示；

（1）首先，我们必须要清楚电流从哪里流出来，必然要流回到哪里去；所以当信号线从0—>1跳变时，这些电流是从哪里来的呢？对于CMOS电平驱动来说，其必然来自于器件的电源管脚VCC；

（2）电流从VCC通过MOS管流向信号线，信号线上的电流不断通过信号路径与回流路径之间的电容，要返回到VCC去；

（3）但是对于信号来说，它并不清楚上面那层是VCC平面，下面那层是GND平面，所以信号边沿只会根据所处的电路结构来决定回流到VCC平面和GND平面的电流大小；
——所谓的电路结构，是指信号线与VCC之间的距离（寄生电容）和信号线与GND之间的距离（寄生电容）大小。

（4）两组信号回流路径如下：

VCC平面作为回流路径（黄色箭头）：VCC平面-输出器件VCC电源管脚，阻抗非常小；
GND平面作为回流路径（绿色箭头）： GND平面-输出信号器件附近的GND平面-去耦电容返-输出器件VCC电源管脚。
——相对回流到VCC平面来说，回流到GND平面的回流反而具有更大的阻抗：去耦电容容抗；当然去耦电容容抗对于高速信号来说也是非常小的，一般10uF陶瓷电容器，理想情况下（不考虑寄生电感）在10MHz的容抗是：|Zc| = |1/jωC | = 1/2πfC = 1.6mΩ；那如果10nF陶瓷电容器（不考虑寄生电感）在100MHz下，容抗也只有160mΩ。所以基本可以忽略不计。

当信号线上的电平由高（1）到低（0）跳变时，其电流通路如下图所示；

（1）当信号线从1—>0跳变时，信号线通过下管MOS管驱动到GND，所以信号线上的电流流回到输出器件内再到器件GND管脚；

（2）那么从信号线上的电流是从哪里来的呢？由上图可以看出，这些电流是从VCC平面和GND平面（回流路径）中来的；电流通过VCC平面和GND平面上寄生电容流向了信号线；
——为什么GND平面也会有电流流向信号线？因为信号线与GND平面间电容起始状态是充满电（有电压差）的，当信号线瞬间降低到0电平，电容两端必须有电流释放出来（GND-信号线方向）；同理信号线与VCC平面之间寄生电容时没有电压差的，当信号线瞬间降低到0电平时，必须进行充电（VCC-信号线方向）；所以VCC平面和GND平面都有电流流向信号线。

（3）电流从哪里来，那它必将回到哪里去；所以它们从VCC和GND平面（回流路径）中出来的电流，必将会从输出器件的GND管脚出发，返回到VCC和GND平面（回流路径）中去；
——电流必将回到信号路径对应的回流路径位置的VCC和GND平面上，我们可以将它看成一个实体的电容器来理解：举个栗子，从电容器的+端输出电流，必将回到它的-端去。

（4）两组信号回流路径如下：

VCC平面作为返回路径（黄色箭头）：从输出器件的GND管脚-去耦电容-输出器件附近VCC平面-VCC电源平面；
GND平面作为返回路径（绿色箭头）：从输出器件的GND管脚-GND平面。

所以，有结论为：从原理上来说：信号的回流路径是GND平面还是VCC平面，是完全等价的。但为什么我们一般都要选择用GND作为回流平面呢？主要原因在于：

在单板上，不同的器件之间的GND一般是同一个，而且会铺有完整的GND平面；
单板上的电源种类有很多，一般不同电源会对电源层进行分割，所以如果以电源平面作为参考，一般情况下会出现回流不连续的情况；
并不是所有的VCC平面都可以作为回流路径的，最好是器件的I/O电源，起码是输出器件的电源；但如果不是输出器件的电源，那么回流路径会出现不连续，导致传输线阻抗不连续。

4，传输线的阻抗与时延

传输线最重要的两个特征是：1，特征阻抗；2，时延（信号传播速率）。

我们知道信号在传输线上传播的过程中，其电压/电流（阻抗）的特性类似电阻，无损传输线可以很好的近似传输线的特征阻抗和时延特性，计算也相对方便，所以先用该模型进行分析。

（1）传输线阻抗

如下图是无损传输线模型，以及在信号传输过程中的电流完整的流动过程，我们用电感L和电容C来描述传输线的回路电感和电容；

L在如下拓扑中，指的是回路电感，这是一个等效电感：不是信号路径的局部电感，而是信号路径与回流路径构成的回路电感；所以该电感跟回流路径强相关。当传输线信号路径不变，而回流路径不连续时（例如：信号线的参考GND层被分割，回流路径就要绕远路），传输线的电感会增大；

C在如下拓扑中，指的是信号路径相对于回流路径之间的电容。
——线与回流地之间的板间电容，其间距是PCB层间距，介电常数是FR-4材料的参数。
我们知道无损传输线的阻抗模型等效为：很多组串联在信号路径上的L和并联在信号路径与回流路径之间的C组成；而且电流是从信号路径到回流路径的方向，由此得出传输线的阻抗可以等效为搭接在信号路径与回流路径的一个电阻（并联电阻）

如上图所示，如果传输线的阻抗是搭在信号路径与回流路径之间的电阻，那么这么多电阻并联后应该是Z0/n而不是Z0。
回到传输线的定义来：信号在传播过程中只有信号前沿的那部分导线才能看成是传输线。

如下图所示，在信号跳变的左侧是高电平（例如3.3V），右侧是低电平（0V），信号路径与回流路径上的电压差保持不变，没有发生充放电的动作，所以这些地方阻抗是无穷大（导线上的信号是固定电平，则信号路径和回流路径之间电压不会变化，此时电容不会进行充放电，所以电流I = 0；而Z =U/I = ∞，相当于断开）；只有处于信号前沿的信号路径与返回路径之间进行着充放电的动作，电容和电感才有了用武之地，成为特征阻抗：Z0。

所以，有结论为：传输线的阻抗是信号前沿（跳变）处所受到的阻抗，它是一个瞬时的阻抗。所以传输线阻抗也可以看成串接在信号路径上的一个电阻。
****传输线阻抗是信号在传输过程中，信号前沿所受到的信号路径与回流路径之间瞬时阻抗****。
如果传输线的瞬时阻抗在整条导线上都保持恒定（传输线瞬时阻抗保持一致），那么我们称之为：传输线的特征阻抗。传输线特征阻抗的特点是：它只与介质材料、传输线结构相关，与传输线长度无关。

（2）传输线时延

传输线时延指的是：信号在传输线上传播过程中，电场与磁场建立的快慢。
信号传输本质上是电磁波的传播，受到介电常数和磁导率的影响，铜线和板材介质相对磁导率是1，不影响信号传播速率，所以信号传播速度主要受到介质介电常数的影响。
在同一介质材料（相同介电常数εr）中信号传输速度V = 1/√(LC)是保持不变的，不会因为导线结构的改变而改变，由于各种情况导致的L或C的改变，可以很好的定性分析对应C和L的变化。

5，有损传输线

实际传输线总是存在损耗的，有损传输线的模型如下图所示，除了串联回路电感和并联电容之外，还有串联电阻和并联电导；传输线的损耗主要就来自于这两部分电阻。

串联电阻是指：金属导线本身的电阻，在直流条件下导线本身电阻是非常小（mΩ级别）；

——随着信号频率的增加，由于趋肤效应导致导线电阻增加，造成导线对信号的损耗。

并联电导是指：导线（信号路径）与回流路径之间的漏电流，由于介质材料是绝缘材料，介质本身电阻非常大，所以在直流条件下电阻非常大（漏电流为nA级别），可以忽略不计；

——随着频率的增加，随着电场变化介质中偶极子运动产生了更大的损耗（介质损耗）。

对于传输信号来说，不管是串联电阻还是并联电导都会造成信号高频分量更大的损耗，高频信号分量损耗的大小决定了传输线的传输带宽；
假定εr在频率中保持不变（实际应用中εr会随频率升高而减小），如下图中α为传输线衰减常数，β为相移常数：

在高频时电阻分量远小于感抗，所以传播速度接近无损传输线；
在低频时电阻分量不可忽略，其传播速度小于无损传输线；
所以信号的高频分量的传播速度要大于低频分量的传播速度，会导致信号上升沿先快后慢。

对于高速信号，我们可以有几个方法来降低传输线损耗的问题：

选用低损耗介质（不是低介电常数）；
尽量减小导线长度；
增加导线宽度，但这会影响差分阻抗，影响差分线之间耦合度。

信号的反射

传输线信号传输的本质是电磁波信号传播，但是其信号反射原理同光的反射/折射完全不同，传输线信号的反射是由于传输线阻抗的变化所导致，而非介质变化引起的。我们知道电磁波的反射会导致其部分能量的损失，所以传输线信号的反射就不可避免的同信号质量联系在一起，我们要尽量避免传输线中间的阻抗不连续点。
且传输信号的目的是：让接收端能正确的接收到信号。很明显假如信号发生了反射，那么根据能量守恒原理，入射信号的能量必然会减小，信号幅度必将发生变化。

1，信号为什么反射

信号沿传输线传播时，路径上每点都有相应的瞬时阻抗，若瞬时阻抗发生变化（阻抗由原先的50Ω变成60Ω），那么部分信号将沿着与原传播方向相反的方向反射，而另外一部分将继续传播。
用物理规则结合数学公式来推导信号反射的原理，当信号沿着传输线从阻抗Z1进入到Z2的边界，此时必须保证在此边界处：V1=V2，I1=I2；同一点的电压和电流必须保持连续：既然交界处电流相等I1=I2，又有I1 = V1/Z1 ，I2 = V2/Z2；从而推导出V1/Z1 = V2/Z2，而Z1 ≠Z2，很显然：V1=V2，I1=I2，I1 = V1/Z1 ，I2 = V2/Z2；这四个等式不能同时满足。
所以，必须在区域1中产生一个反射回源端的电压，它唯一的目的是吸收入射信号和传输信号不匹配的电压和电流。

如上图所示，那我们用V入射，V反射，V传输来表示信号在阻抗交界面产生的电压，其对应的电流分别是I入射，I反射，I传输；电流和电压关系需满足：V入射+V反射=V传输；I入射-I反射=I传输；那么，V入射/Z1 - V反射/Z1 = V传输/Z2；再由 V入射/Z1 - V反射/Z1 = （V入射+V反射）/Z2；可得：
$$
ρ = V反射/V入射=（Z2-Z1）/（Z2+Z1）；t = V传输/V入射= 2*Z2/（Z2+Z1）。
$$
——ρ：反射系数；t：传输系数。

从下图传输线信号传输模型来定性理解阻抗突变导致的反射现象，假设Z0=50ohm，Z1=100ohm，输入电压V=5V；传输线电流在阻抗突变交接前电流是：5V/50ohm = 100mA；由于传输线上存在电感，电流不能突变，考虑极端情况：100mA全部电流涌入Z1（100ohm），那么此处会产生电压V2 = 100ohm*100mA = 10V，此时传输（Z1）电压大于入射（Z0）电压5V，那么必将产生一个反射电流I反= (5V-10V)/50ohm = -100mA。而在实际情况中，当电压上升到大于5V后，电感两端产生反向电压，正向流入的电流迅速减小，同时产生反射电流/电压，传输电流不会上升到100mA的极限值，最终形成一个平衡。

2，低源端阻抗无匹配传输线

假设驱动器内阻为10ohm，无损传输线阻抗为50ohm，终端阻抗∞（开路/无匹配）；信号传输的过程如下：

信号从源端发出电压沿着传输线传输，从传输线模型可知此时驱动器内阻与传输线阻抗形成分压关系，V源端1 = [50/(10+50)]*1V = 0.84V；
经过阻抗连续的无损传输线，Td = 1ns的延时，信号V源端1无损耗的传播到终端，信号幅度为0.84V；
此时在终端开路，阻抗为∞，传输线阻抗不连续而发生发射，反射系数为：(∞-50)/(∞+50) = 1，表示全反射；终端电压幅度V终端1 = 0.84V+0.84V=1.68V，此时有0.84V电压从终端反射回源端；
信号到达源端后，源端阻抗为10ohm，注意反射回源端时这个10ohm是并联在电源轨道上，此时电源等价于回流路径，所以不是分压而是反射；反射系数为：（10-50）/（10+50）= -0.667，反射电压 V源端反射1 = 0.84V*（-0.667）= -0.56V， V源端2 = 0.84+0.84V–0.56V=1.12V；
V源端反射1 电压（-0.56V）经传输线再传输到终端，终端全反射，所以终端电压V终端2 =1.68V-（0.56V*2）= 0.56V；
同理-0.56V（反射电压）再传输回源端，至此形成一个振荡，其振荡频率为传输线延时的4倍；振荡幅度不断衰减直至输出信号电压1V。
下面探讨几个问题

（1）为什么是源端信号最初发出来的信号与特征阻抗是分压关系？

如下图所示，当一个高电平信号Vo刚刚从器件中发出，它首先是经过了一个串联的内阻Zs；
——如果外接了源端串联匹配电阻，那么Zs包括匹配电阻，要求是串联匹配电阻与芯片之间的距离满足集总模型长度（即，走线长度要小于1/10的信号波长），这也是为什么源端匹配尽量靠近发送端的原因。
信号传播到传输线上后，受到一个传输线的特征阻抗Z0，我们上一章已经说明了，Z0是信号路径相对于回流路径的阻抗（即如下图），并非如源端的阻抗（内阻和源端匹配）是串在信号路径上的；
现在就是一个非常简单的计算了，V1 = Vo*Z0/(Zs+Z0)。

（2）第二个问题是：为什么信号在理想传输线的传输过程中不会产生反射呢？

如下图所示，假设信号在传播过程中，从第2个Z0切换到了第3个Z0，此时传输线上的电流并不会发生变化，即电流一直处于连续状态，所以电压也不会发生变化；
——如下示意图中，特征阻抗是分离开的一个个Z0，这只是为了便于理解；实际传输线上的特征阻抗并非是离散的，而是随着信号边沿的传播过程而非常连续的：当信号边沿连续从左往右传播时，一部分传输线结束了充放电（L+C），另一部分则开启了充放电（L+C）。

Hx(ω) = exp √{-x[(R(ω) + jωL)*(jωC) ]}，传输线传递函数，包含传输线损耗和延时；
T(ω)= [2*ZL(ω)]/[ZL(ω)+Z0(ω)]，终端传输系数
——传输系数，即传输过去的信号幅度比例。
R2(ω) = [ZL(ω)-Z0(ω)]/[ ZL(ω)-+Z0(ω)]，终端反射函数；终端反射是如何发生的呢？

如下图所示，当信号传输至终端时，原来传输线上的电流I0 = V0/Z0，但是ZL > Z0的话：IL = V0/ZL，此时IL < I0，必然会多出一部分电流没地方去，只能原路返回。
——假如ZL为无穷大，那么这些电流没地方流出去，只能全部返回回来，所以此时的电流I = 2$\times$I0，那我们可以根据欧姆定律得到电压V = 2$\times$I0$\times$Z0 = 2$\times$V0；这是全反射的情况。

R1(ω) = [Zs(ω)-Z0(ω)]/[ Zs(ω)-+Z0(ω)]，源端反射函数。

如下图所示，当从终端反射回来的信号边沿到达源端，源端阻抗Zs是一端连接至Vcc或GND的；
如果Zs是接到GND（即，输出驱动为低），那么就比较好理解，它在电路结构中的位置等价于特征阻抗Z0和终端阻抗ZL，所以其也是有传输系数和反射系数的；
如果Zs是连接到VCC（即，输出驱动为高），需要摒弃回流是GND的这种错误观念，在信号回流上VCC和GND是等价的，VCC就可以当做GND。

3，短线模式下的传递模型

当输入信号的边沿时间足够长（线长<1/6 Tr），所有错开振荡部分会混合叠加，不会产生振铃现象，仅当信号上升时间能够与信号在传输线上的延迟差不多甚至更小时（长线），才会出现明显的过冲和振铃。
根据如上的理论推导，在短线模式下传输线的损耗和延时都可以忽略不计，且T(ω)= R2(ω)+1；可以将传输函数简化：Sshort(ω)= [A(ω)$\times$(R2(ω)+1)]/[1-(R2(ω)$\times$R1(ω)] ，将函数代入源端阻抗Zs，传输线阻抗Z0，终端阻抗ZL计算，Sshort(ω) = ZL/(ZL+Zs)。
得到一个重要的结论：在短线模式下的传输模型是由负载阻抗ZL和源端阻抗Zs构成的简单阻抗分配网络。
——源端串联阻抗匹配有用么？当然有用，串阻叠加到Zs上，从而减小接收端信号电压幅度。

4，高源端阻抗无匹配传输线

源端阻抗值大，主要体现在源端阻抗分压：A(ω) =Z0(ω)/[Zs(ω)+Z0(ω)] 和源端反射系数：R1(ω) = [Zs(ω)-Z0(ω)]/[ Zs(ω)+Z0(ω)]上，而传输到终端后反射系数：R2(ω) = [ZL(ω)-Z0(ω)]/[ ZL(ω)+Z0(ω)] = 1，是全反射（因为理想终端阻抗ZL(ω)是无穷大）。

此时由于Zs（ω）很大导致A(ω)很小，所以高源端阻抗时初始输出的阶跃非常小；
假如源端阻抗Zs(ω)=1000Ω，特征阻抗Z0(ω) = 50Ω，那么源端分压A(ω) = 50/(1000-50) = 1/19，如果是3.3V电平信号，那么在经过第一次阻抗分压之后的电压是0.17V。
R1(ω)很大说明信号从终端反射回源端时也产生了较大幅度反射，在确定的时间段内，其最终值等于输入阶跃值；
——根据上面的栗子：R1(ω) = (1000-50)/(1000+50) = 950/1050 = 0.9，注意：反射系数为0.9表示很大的反射（全反射的系数为1），如果反射系数为0表示没有反射，反射系数为-1表示全吸收。
如下图所示，我们可以得到这种阶跃非常像RC滤波的响应（缓慢的上升，类似于RC充电），阶跃响应的建立时间段与源阻抗和线上负载电容的乘积相近；由于高源端阻抗无匹配传输线阶跃响应与RC滤波的相似性，可以把传输线的输入看做容性负载，所以在线路匹配设计时，如果串入电阻过大时，现象是：无过冲，但边沿会变缓。

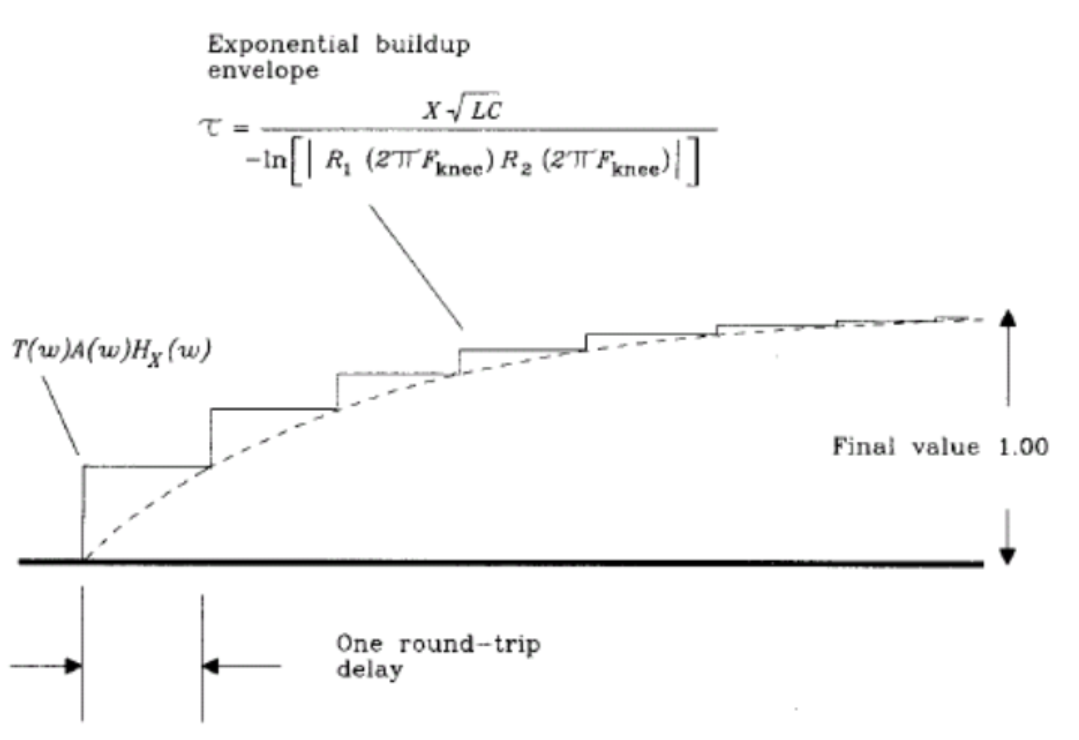
5.中间容性负载传输线

容性负载不仅仅表现为接收器的输入电容，而且还表现在类似于容性结构的负载，如芯片引脚较宽的焊盘也类似于一个容性负载，对于低速信号，过孔也可以粗略地看作是一个容性负载。

当容负载处于传输线中间时，从电容两端看向电路的其他部分，可等效成下图所示的形式。

如果两侧传输线阻抗都是Z0 =50Ω，则信号到达电容时相当于通过一个25Ω电阻对其充电。假设入射电压最大值为U，电容两端电压为
$$
V_c = U \left( 1 - e^{-\frac{t}{\tau}} \right)
$$
下图显示了电容两端的电压和通过电容的电流曲线。曲线形式与传输线末端电容类似，只不过这里的时间常数为$\tau = \frac{Z_0}{2} C = (25 \times 8) , \text{ps} = 200 , \text{ps}, ; t = 1 , \text{ns}$时信号到达电容，开始对电容充电，经过τ=200ps电容电压上升到632 mV，是其终值电压的63.2%。下图为电容阻抗曲线，电容经过τ·ln2=138.6ps后达到等效阻抗25Ω。

6，等间隔容性负载传输线

有一种电路模型，与原来的模型相比有相同的电感和电阻，但有不同的电容值；一驱多的DDR/Nand Flash 拓扑结构，每片DDR/Nand Flash颗粒相当于增加了一个容性负载；我们将这个容性负载值加到现存传输线的单位长度电容上，得到新的传输线模型电容值。
如下图所示，此时得到一个重要的结论：等间距多容性负载新模型的传输线阻抗会变小，传输延时会增加，在阻抗匹配和时序设计时要另外考虑。
——传输线上信号传播速度和特征阻抗取决于在传输过程中受到感抗和容抗的组合： Z = LC，介电常数和磁导率只是这两个参数的另外一种方式的呈现，所以虽然介电常数和磁导率不变，如果还有其它外部条件改变了信号传播过程中的感抗和容抗，那么还是会影响到其传播速度和传输线阻抗。

7，直角转弯传输线

当走线是直角时：直角弯曲导线的有效宽度增大了，从而产生了不需要的额外寄生电容，就像是附在传输线上的一个容性负载。有了这个容性负载传输线的瞬时阻抗将会发生变化（产生阻抗不连续点），根据中间容性负载传输线章节所述，在此会产生一个反射，影响信号质量。

如上图所示，解决传输线直角的问题，有两种解决方案：

将直角做成圆角，是的传输线的宽度保持固定，改善信号反射以及信号上升沿时间的不良影响；
对直角进行斜切（45°），计算上升沿时间常数（如右下图），这个上升时间的值很小，可以满足上升沿大于100ps（差不多对应10GH以内的信号）的高速信号应用。

传输线阻抗匹配

要使信号从源端完整的传输到终端，那么有三种方式：

短线模式传输函数：Sshort(ω)= ZL/(ZL+Zs)；
源端匹配传输函数：S源端 = Hx(ω)；
终端匹配传输函数：S终端 = A(ω)*Hx(ω)；

1，源端匹配

源端匹配的意思是：Zs = Z0，即源端串联电阻后使得阻抗等于传输线特征阻抗。那这样有什么好处呢？

阻抗分压：A(ω) = Z0(ω)/[ Zs(ω)+Z0(ω)] = 1/2，信号从源端发出来幅度减半；
假设终端负载阻抗ZL为高阻（即∞），那么可得到终端反射系数：R2(ω) = [ZL(ω)-Z0(ω)]/ [ZL(ω)+Z0(ω)] = 1，即全反射，信号幅度是输入到终端信号幅度的2倍，算上源端发出来的1/2，刚好是输出的信号幅度；
源端阻抗的反射系数：R1(ω) = [Zs(ω)-Z0(ω)]/ [Zs(ω)+Z0(ω)] = 0，即，当信号从终端反射回到源端时，信号被全部吸收；
——信号从终端反射回来后，将不会再被反射到终端去，信号传输过程结束。
传输线的传输函数：S源端 = A(ω)$\times$Hx(ω)$\times$[ R2(ω)+1]；将A(ω)=1/2， R2(ω)=2代入传输线的传输函数；所以得到传输函数：S源端 = Hx(ω)。
——从信号的传输函数可以看到，终端接收到的信号相比于源端只是传输线本身的衰减，不会由于阻抗不连续而产生过冲等。

关于源端匹配的问题：

我们是否需要等待信号传输以及反射流程全部走完（2T），才能发起下次的信号传输？
从传输线的定义：传输线传播的只是信号的边沿，即，只有信号边沿所在位置的导线才是传输线；所以一旦信号边沿离开了源端，那么靠近源端的部分导线处于空闲状态，就可以马上发起下一次的信号传输，两者不会相互干涉；

那从终端反射回来的1/2幅值信号边沿，是否会影响到下一个传输的信号呢？
第二个信号与反射回的信号在相遇时会产生叠加，但是他们传播的方向不同，叠加后会相互穿越，之后还是各自保持原先的信号幅值继续传播。

2，终端匹配

（1）终端并联匹配

并联匹配如下图所示有如下特点：

假设源端输出阻抗很小(Zs≈0，A(ω)≈1),那么在传输线上是全幅值传播；
——源端串联匹配的第一次传输是半幅值，但若Zs很小时，第一次传输的信号基本上就是全幅值。
所有反射波形在终端被并联匹配电阻抑制（R1=Z0）；
——如上分析，当线路阻抗匹配时，则不会产生反射。
接收端电压 = 发送端电压，只有传输线延时。

从上述分析，终端并联匹配的信号传输模型更简单，传输线上所有位置的信号相等（不会出现半高电平），同时传输线充电常数比源端匹配小一半，简直就是完美的匹配拓扑。但为什么我们在实际应用中，却使用源端匹配更多呢？
假设输出LVTTL电平（3.3V），传输线阻抗为50ohm，所以需要在终端匹配：50ohm电阻至GND；那么在输出3.3V高电平时，在50ohm电阻上流过的电流是：3.3V/50 = 66mA，且终端匹配电阻上消耗功率P = 3.3 *0.066= 0.22W；这将导致如下3个问题：